Multi-Objective Optimization with apsimNGpy
In real-world agricultural systems, most objectives—such as maximizing crop yield while minimizing environmental impact—are inherently conflicting. These trade-offs cannot be effectively addressed using single-objective optimization algorithms, which are limited to optimizing one goal at a time. Fortunately, multi-objective optimization algorithms inspired by evolutionary principles are well-suited to handle such complexity by exploring a range of trade-offs between competing objectives.
This tutorial demonstrates how to perform multi-objective optimization on an APSIM Next Generation model using the apsimNGpy.optimizer.moo module. You will learn two ways to define decision variables and how to apply evolutionary algorithms via the pymoo library. This approach allows you to explore and analyze trade-offs among competing objectives, such as productivity and sustainability, in a robust and flexible way.
Prerequisites
Make sure you have the following installed and configured:
APSIM Next Generation installed
Python 3.10+
apsimNGpy package (latest version)
Python packages:
pymoo,matplotlib,numpy, andpandas
Step 1: Import required modules
from apsimNGpy.optimizer.moo import MultiObjectiveProblem, compute_hyper_volume, NSGA2
from pymoo.optimize import minimize
import matplotlib.pyplot as plt
from apsimNGpy.core.apsim import ApsimModel as Runner
Interpretation
ApsimModelhandles model simulation and editing. It is an apsimNGpy classMultiObjectiveProblemwraps your problem into a multi-objective oneNSGA2: a multi-objective genetic algorithmminimize()will be used to minimize the objectives in the finals steps
Step 2: Initialize the APSIM model runner
You create a runner tied to a specific .apsimx model file. This runner manages simulation and parameter editing.
Here, I a using the default maize template. Because it does not have nitrate leaching in its Report table, I have also added it.
runner = Runner("Maize")
runner.add_report_variable('[Soil].Nutrient.NO3.kgha[1] as nitrate', report_name='Report')
For more runner API details, check the link below
ApsimModel API: ApsimModel
Step 3: Define Objective Functions
Objective functions take APSIM output (as a DataFrame) and return scalar values. You can define any number of such functions depending on the goals. If you have 3 objectives, then we expect 3 functions.
Important
Maximization objectives must be converted into minimization form by negating them (e.g., -f(x)), since the underlying optimization algorithms are designed to minimize objective functions.
def maximize_yield(df):
return -df['Yield'].mean()
def minimize_nitrate_leaching(df):
return df['nitrate'].sum()
Step 4a: Define decision variables (Approach 1 - direct List)
You can directly supply a list of variables to optimize as follows:.
decision_vars = [
{'path': '.Simulations.Simulation.Field.Fertilise at sowing',
'Amount': "?", 'bounds': [50, 300], 'v_type': 'float'},
{'path': '.Simulations.Simulation.Field.Sow using a variable rule',
'Population': "?", 'bounds': [4, 14], 'v_type': 'float'}
]
# initialise the problem
problem = MultiObjectiveProblem(runner, objectives=[maximize_yield, minimize_nitrate_leaching], decision_vars=decision_vars)
Each dictionary defines:
path: the APSIM model path to the component.Amount/Population: the parameter to be optimized (denoted by ‘?’).bounds: lower and upper bounds for the optimizer.v_type: variable type.
Note
Each decision variable specification must contain exactly one parameter marked with '?'. This signifies the target parameter to be optimized during the calibration or search process.
Step 3b: Define decision variables (Approach 2 - using add_control())
Instead of a list, you can add each parameter one at a time. There is a need to initiate our problem with objectives only, then add control variables on the fly.
# initialise the problem
problem = MultiObjectiveProblem(runner, objectives=[maximize_yield, minimize_nitrate_leaching])
problem.add_parameters(
path='.Simulations.Simulation.Field.Fertilise at sowing',
Amount='?', bounds=[50, 300], v_type='float')
problem.add_parameters(
path='.Simulations.Simulation.Field.Sow using a variable rule',
Population='?', bounds=[4, 14], v_type='float')
Note
The best approach depends on the user’s preference, but the last approach helps the user to focus on one control variables required details at a time.
Step 5: Run the NSGA-II optimizer
NSGA-II is a commonly used algorithm for multi-objective problems. There are other genetic multi-objective algorithms, but for trade-off analysis with APSIM,
NSGA-II is more than adequate. You can now run it as follows:
algorithm = NSGA2(pop_size=20)
result = minimize(
problem.get_problem(),
algorithm,
('n_gen', 10),
seed=1,
verbose=True
)
pop_size: number of candidate solutions per generation.n_gen: number of generations to run.
Step 6: Plot the Pareto Front
The results show trade-offs between competing objectives. You can visualize them:
F = result.F
plt.scatter(F[:, 0]* -1, F[:, 1])
plt.xlabel("Yield")
plt.ylabel("N Leaching")
plt.title("Pareto Front")
plt.show()
Tip
Compute Hyper volume (Optional)
The hyper volume gives a scalar metric of solution quality, and can be useful if you want to explore the best inputs such as pop_size, max_gen.
A high value indicates better solution quality than a lower one. Therefore, it can also be used to compare the performance of multiple minimization algorithms.
hv = compute_hyper_volume(F, normalize=True)
print("Hyper volume:", hv)
Hint
Objectives are typically expressed in different units, and some—such as yield—may have much larger amplitudes. This makes determining a suitable reference point challenging. In such cases, normalization can help automatically detect the reference point by applying specific thresholds.
Attention
While multi-objective algorithms like NSGA-II can technically handle single-objective problems, doing so is like using an axe to slice an orange or shooting a mosquito with an m16 —it’s overkill. Simpler and more efficient algorithms are better suited for single-objective optimization tasks.
Comparing objectives without mult-objective optimization
What if we just run out the different combinations of the decision variables: population density and the nitrogen application rate can we ge the same pareto front and trade-offs we have seen in that graph? To answer this question we are going to run a factorial experiment.
import numpy as np
population = [str(i) for i in np.random.randint(low=1, high=12, size=20)]
nitrogen = [str(i) for i in np.random.randint(low=50, high=300, size=20)]
runner.create_experiment(permutation=False, base_name='Simulation')
runner.add_factor(specification=f"[Fertilise at sowing].Script.Amount = {','.join(nitrogen)}", factor_name='Nitrogen')
runner.add_factor(specification=f"[Sow using a variable rule].Script.Population ={','.join(population)}",
factor_name='Population')
runner.run(verbose=True)
df = runner.results.drop_duplicates()
df = df.groupby('SimulationID')[['Yield', 'nitrate']].mean()
yi = df.Yield
nitrate =df.nitrate
plt.scatter(yi , nitrate)
plt.xlabel("Yield")
plt.ylabel("N Leaching")
plt.title("Trade-offs between yield and nitrate leaching")
plt.show()
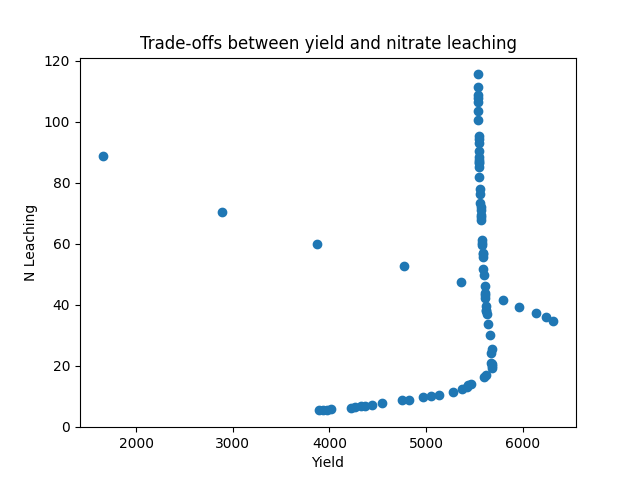
comment
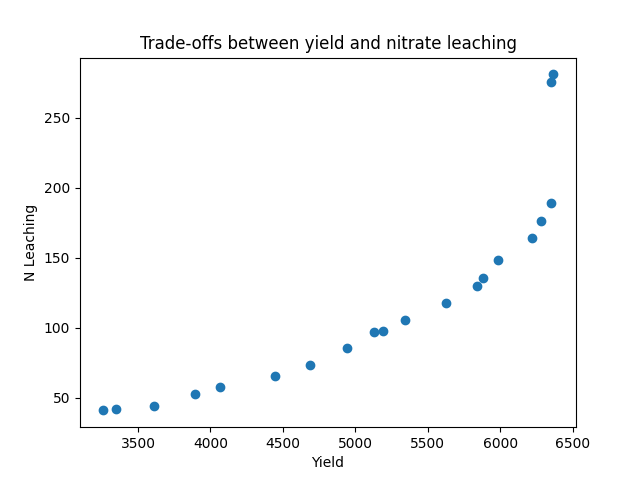
From the graph above, it is clear that the pattern is no where close to what we could call a clear pareto front that can demonstrate the trade-offs between different objectives.
comment
From the graph above, it is clear that achieving high corn yield while simultaneously reducing nitrate leaching is quite challenging. This is because high yields typically require the application of large amounts of nitrogen fertilizer, which is often associated with increased nitrate leaching.